Факультет Математики и Информатики ГрГУ: Разновидности фракталов

Вход

Поиск по сайту

Google на mf.grsu.by

Главная страница >> Студенту >> Личные страницы >> О Фракталах >> Разновидности фракталов

Разновидности фракталов:

Классификация фракталов:

Геометрические фракталы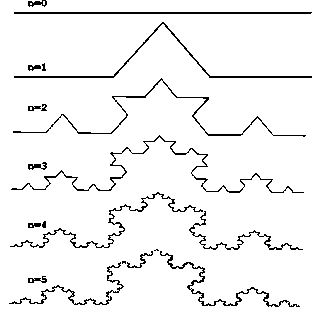

Алгебраические фракталы

Стохастические фракталы

Множество Мандельброта

Множество Жулиа

Биоморфы

Классификация фракталов.

Для чтобы представить все многообразие фракталов удобно прибегнуть к их общепринятой классификации.

Геометрические фракталы

Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.

Рис 1. Построение триадной кривой Кох.
Рассмотрим один из таких фрактальных объектов - триадную кривую Кох. Построение кривой начинается с отрезка единичной длины (рис.1) - это 0-е поколение кривой Кох. Далее каждое звено (в нулевом поколении один отрезок) заменяется на образующий элемент, обозначенный на рис.1 через n=1. В результате такой замены получается следующее поколение кривой Кох. В 1-ом поколении - это кривая из четырех прямолинейных звеньев, каждое длиной по 1/3. Для получения 3-го поколения проделываются те же действия - каждое звено заменяется на уменьшенный образующий элемент. Итак, для получения каждого последующего поколения, все звенья предыдущего поколения необходимо заменить уменьшенным образующим элементом. Кривая n-го поколения при любом конечном n называется предфракталом. На рис.1 представлены пять поколений кривой. При n стремящемся к бесконечности кривая Кох становится фрактальным обьектом.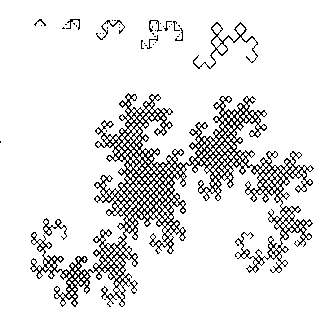

Рис 2. Построение "дракона" Хартера-Хейтуэя.
Для получения другого фрактального объекта нужно изменить правила построения. Пусть образующим элементом будут два равных отрезка, соединенных под прямым углом. В нулевом поколении заменим единичный отрезок на этот образующий элемент так, чтобы угол был сверху. Можно сказать, что при такой замене происходит смещение середины звена. При построении следующих поколений выполняется правило: самое первое слева звено заменяется на образующий элемент так, чтобы середина звена смещалась влево от направления движения, а при замене следующих звеньев, направления смещения середин отрезков должны чередоваться. На рис.2 представлены несколько первых поколений и 11-е поколение кривой, построенной по вышеописанному принципу. Предельная фрактальная кривая (при n стремящемся к бесконечности) называется драконом Хартера-Хейтуэя.
В машинной графике использование геометрических фракталов необходимо при получении изображений деревьев, кустов, береговой линии. Двухмерные геометрические фракталы используются для создания объемных текстур (рисунка на поверхности обьекта).

Алгебраические фракталы

Это самая крупная группа фракталов. Получают их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы. Интерпретируя нелинейный итерационный процесс, как дискретную динамическую систему, можно пользоватся терминологией теории этих систем: фазовый портрет, установившийся процесс, аттрактор и т.д.
Известно, что нелинейные динамические системы обладают несолькими устойчивыми состояниями. То состояние, в котором оказалась динамическая система после некоторого числа итераций, зависит от ее начального состояния. Поэтому каждое устойчивое состояние (или как говорят - аттрактор) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния. Таким образом фазовое пространство системы разбивается на области притяжения аттракторов. Если фазовым является двухмерное пространство, то окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы (итерационного процесса). Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные нетривиальные структуры.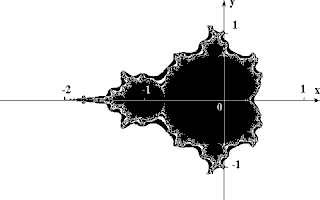

Рис 3. Множество Мандельброта.
В качестве примера рассмотрим множество Мандельброта (см. pис.3 и рис.4). Алгоритм его построения достаточно прост и основан на простом итеративном выражении:

Z[i+1] = Z[i] * Z[i] + C,

где Zi и C - комплексные переменные. Итерации выполняются для каждой стартовой точки C прямоугольной или квадратной области - подмножестве комплексной плоскости. Итерационный процесс продолжается до тех пор, пока Z[i] не выйдет за пределы окружности радиуса 2, центр которой лежит в точке (0,0), (это означает, что аттрактор динамической системы находится в бесконечности), или после достаточно большого числа итераций (например 200-500) Z[i] сойдется к какой-нибудь точке окружности. В зависимости от количества итераций, в течении которых Z[i] оставалась внутри окружности, можно установить цвет точки C (если Z[i] остается внутри окружности в течение достаточно большого количества итераций, итерационный процесс прекращается и эта точка растра окрашивается в черный цвет).

Рис 4. Участок границы множества Мандельброта, увеличенный в 200 pаз.
Вышеописанный алгоритм дает приближение к так называемому множеству Мандельброта. Множеству Мандельброта принадлежат точки, которые в течение бесконечного числа итераций не уходят в бесконечность (точки имеющие черный цвет). Точки, принадлежащие границе множества (именно там возникает сложные структуры) уходят в бесконечность за конечное число итераций, а точки лежащие за пределами множества, уходят в бесконечность через несколько итераций (белый фон).

Стохастические фракталы

Еще одним известным классом фракталов являются стохастические фракталы, которые получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные - несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.

Существуют и другие классификации фракталов, например деление фракталов на детерминированные (алгебраические и геометрические) и недетерминированные (стохастические).

Множество Мандельброта

Фракталом Мандельброта названа фигура, которая пораждается очень простым циклом. Для создания этого фрактала необходимо для каждой точки изображениявыполнить цикл итераций согласно формуле: Z_k+1 = Z_k² + Z₀ где k = 0, 1, ...,n. Величины Z_k - это комплексные числа, Z_k = x_k+ i*y_k, причём стартовыезначения x₀ и y₀ - это координаты точки изображения. Для каждой точки изображения выполняются ограниченной количество раз(n) или до тех пор, пока модуль числа Z_k не превышает m.
Ниже приводится алгоритм построения множества. Работа с палитрой объясняется здесь.
Program Fractal;
Uses
   Crt, Graph;
Const
   a = 0.0;
   b = 0.0;
Var
   Gd, Gm : Integer;
   i, j : Integer;
   r, x, x1, y, y1 : Real;
   col : Word;
Begin
{Инициализируем палитру на 256 цветов}
asm
   mov ax ,13h
   int 10h
end;
For i:=1 To 15 Do
Begin
    Port[$3c8]:=i;
    Port[$3c9]:=i*4;
    Port[$3c9]:=0;
    Port[$3c9]:=0;
End;
For i:=16 To 32 Do
Begin
    Port[$3c8]:=i;
    Port[$3c9]:=63;
    Port[$3c9]:=(i-16)*4;
    Port[$3c9]:=0;
End;
For i:=33 To 47 Do
Begin
    Port[$3c8]:=i;
    Port[$3c9]:=63;
    Port[$3c9]:=63;
    Port[$3c9]:=(i-33)*4;
   End;
For i:=48 To 255 Do
Begin
    Port[$3c8]:=i;
    Port[$3c9]:=63;
    Port[$3c9]:=63;
    Port[$3c9]:=63;
End;
For i := -160 To 160 Do
    For j := -100 To 100 Do
    Begin
      x := i/100;
      y := j/100;
      r := 0;
      col := 0;/*проверка на выход из цикла*/
      While (r < 12) Do /*проверка на выход из цикла*/
      Begin
        x1 := x*x-y*y + (i/100) ; /*находим квадрат исходного комплексного числа*/
        y1 := 2*x*y + (j/100) ; /*плюс число-переменная*/
        r := SQRT(x1*x1 + y1*y1); /*находим модуль нового полученного числа*/
        Inc(col); /*увеличиваем значение числа итераций*/
        If (x = x1) And (y = y1) Then/*проверка на зацикливание*/
          r := 13; /*эктренный выход из цикла при зацикливании*/
        If (col > 255) Then /*ещё одна проверка на зцикливание*/
          r := 1000; /*экстренный выход*/
        x := x1; /*переопределение комплексных*/
        y := y1; /*координат*/
      End;
      Mem[$0a000:(j+100)*320+(i+160)] := col; /*ставим точку полученного цвета*/
    End;
    readln;
End.

Множество Жулиа

Фрактал Жулиа внешне совсем не похож на фрактал Мандельброта, однако он определяется итерационным циклом, почти полностью тождественным с циклом генерации Мандельброта. Формула итераций для фрактала Жулиа такая:
Z_k+1 = Z_k² + c, где c - комлексная константа. Условием завершения итераций является |Z_k| > 2 - в классическом варианте.
Program Gull;
Uses
Crt, Graph;
Const
a = 0.4; {0.1 0.4 0.3 0.0 0.366}
b = -0.3; {0.0 0.3 0.0 0.3 0.366}
Var
Gd, Gm : Integer;
i, j : Integer;
r, x, x1, y, y1 : Real;
col : Word;
Begin
asm
mov ax ,13h
int 10h
end;
for i:=1 to 15 do
begin
Port[$3c8]:=i;
Port[$3c9]:=i*4;
Port[$3c9]:=0;
Port[$3c9]:=0;
end;
for i:=16 to 32 do
begin
Port[$3c8]:=i;
Port[$3c9]:=63;
Port[$3c9]:=(i-16)*4;
Port[$3c9]:=0;
end;
for i:=33 to 47 do
begin
Port[$3c8]:=i;
Port[$3c9]:=63;
Port[$3c9]:=63;
Port[$3c9]:=(i-33)*4;
end;
for i:=48 to 255 do
begin
Port[$3c8]:=i;
Port[$3c9]:=63;
Port[$3c9]:=63;
Port[$3c9]:=63;
end;
For i := -160 To 160 Do
For j := -100 To 100 Do
Begin
x := i/100;
y := j/100;
r := 0;
col := 0;
While (abs(r) < 2) Do
Begin
x1 := x*x - y*y + a;
y1 := 2*x*y + b;
r := SQRT(x1*x1 + y1*y1);
Inc(col);
If (x = x1) And (y = y1) Then
r := 11;
if (col > 255) then
r := 3;
x := x1;
y := y1;
End;
Mem[$0a000:(j+100)*320+(i+160)] := col;
End;
readln;
End.

Биоморфы

Итак, мы рассматриваем в цикле (точнее, в двух циклах, по x и по y) точки плоскости в выбранном диапазоне. Каждую точку превращаем в комплексное число, получая действительную составляющую (RE) из координаты по х и мнимую составляющую (IM) из координаты по y с помощью масштабного коэффициента. Для возведения комплексного числа в квадрат применим подпрограмму QWA. Поясним, как получились ее формулы. Запишем комплексное число в виде z=a+bi, где a и b его дейстительная и мнимая составляющие. Найдем квадрат этого числа: z2=(a+bi)*(a+bi)=a2+abi+abi+(bi)2=a2+2abi-b2=(a2-b2)+2abi или в наших символах re1=re*re-im*im - действительная часть после возведения в квадрат im1=2*re*im - мнимая часть после возведения в квадрат. Теперь открываем цикл (со счетчиком v), в теле которого возводим число в квадрат, вызывая QWA, потом добавляем фиксированное число к каждой составляющей комплексного числа, потом проводим анализ для выхода из цикла, например, по достижению переменными re и im какого либо значения. Значение счетчика цикла v запоминается и именно оно служит для определения цвета в данной точке. В этом и состоит изюминка алгоритма получения красивого изображения - разные точки выходят при разных значениях счетчика и группируются по цветам в замысловатые узоры. После выхода из цикла еще вводим условия для рисования цветом v, а остальные области заполняем черным цветом. Теперь, подбирая масштаб, фиксированное число (точнее две его составляющие), условие выхода и условия рисования получим картинку, соответствующую приведенному листингу программы.
PROGRAM biomorph;
USES CRT,GRAPH,DOS;
LABEL 1;
VAR
RE,IM,RE1,IM1 : REAL ;
V,M,T,SIZE,X,
Y,KX,KY,X1,Y1,
KX1,KY1,Z,Z1,
X2,Y2 : INTEGER;
JJ,W,I,R1,R2,
R3,ROP,X36,Y36,
X72,Y72,B,D : INTEGER ;
B1,K,J,I1,I2,
I4,I3,I5,I6 : INTEGER ;
C,S1 : STRING;
P : POINTER ;
Q,E,RR : REAL ;
procedure GrInit;
var
GraphDriver : Integer;
GraphMode : Integer;
ErrorCode : Integer;
begin
GraphDriver:= Detect;
InitGraph(GraphDriver,GraphMode,'');
ErrorCode:=GraphResult;
End;
PROCEDURE QWA ;
BEGIN
RE1:=RE*RE-IM*IM ; IM1:=2*RE*IM ; RE:=RE1 ; IM:=IM1 ;
END ;
PROCEDURE KUB ;
BEGIN
RE1:=RE*(RE*RE-3*IM*IM);
IM1:=IM*(3*RE*RE-IM*IM);
RE:=RE1 ; IM:=IM1;
END ;
{+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++}
BEGIN
GRINIT; SETFILLSTYLE(1,15);
BAR(0,0,640,480);
X:=-320 ;
REPEAT Y:=-240 ;
REPEAT V:=0;
RE:=-1.+0.001*X;
IM:=0+0.001*Y ;
REPEAT KUB;
RE:=RE+1.00003;
IM:=IM+1.01828201638 ;
IF RE*RE > 50 THEN
GOTO 1 ;
IF IM*IM > 50 THEN
GOTO 1;
V:=V+1 ;
UNTIL V>40 ;
1: IF ( ABS(RE) > 10 ) OR ( ABS(IM) > 1000) THEN
BEGIN
PUTPIXEL((X+320),(Y+240),TRUNC(V+8));
END
ELSE
PUTPIXEL((X+320),(Y+240),0);
Y:=Y+1 ;
UNTIL Y > 241 ;
X:=X+1 ;
UNTIL X>320 ;
C:=READKEY;
CLOSEGRAPH;
END.