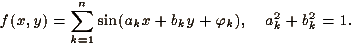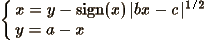|
|


Красивые картинки с математическим
содержанием.
 |
| Ref: Science, 1987, © 3, стр. 72-75. |
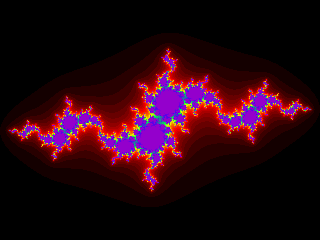
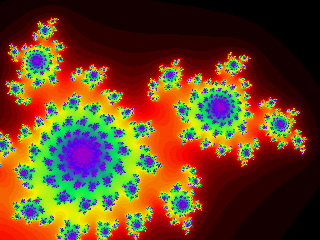
Это - множество Жюлиа. Цвет каждой точки
зависит от того, сколько итераций комплексной функции
может быть сделано, пока точка z не
выйдет за пределы круга радиуса r (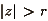 ). Здесь ). Здесь 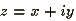 - комплексное
число, соответствующее точке - комплексное
число, соответствующее точке .gif) . Множество
Жюлиа - это множество таких точек, что отображения вида . Множество
Жюлиа - это множество таких точек, что отображения вида
не отображают их в окрестность бесконечности. На
картинках эти точки окрашены лиловым цветом (и точки, достаточно близкие к
ним).
Так, например, если a = 1, и
b = 0, то множеством Жюлиа будет являться открытый
единичный круг с центром в нуле.
Нижняя же картинка получена выбором
параметров
a = 1.8, и
b = 0.2 i. |
 |
Здесь изображено множество Мандельброта
(окрашено лиловым цветом). Картинка получается с помощью той же процедуры,
что и выше. Различие состоит в том, что начальное значение для точки
z берётся всегда равным нулю, а точке с координатами .gif) на картинке
соответствует комплексный параметр
b = x + y i. на картинке
соответствует комплексный параметр
b = x + y i.
|
 |
| Origin: Квант, 1987, © 11, стр. 21. |
Цвет каждой точки на этой картинке определяется по формуле
(x2 + y2) /
S mod 16.
Картинка выглядит как объединение семейства периодических картинок с
окружностями. Что служит причиной этого эффекта - никому пока
неизвестно. |
 |
Здесь изображены линии уровня собственной функции оператора Лапласа.
Такие собственные функции имеют вид
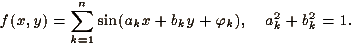
Картинка построена для случая n=5.
Кстати,
не кажется ли вам эта картинка трехмерной? :) |
 |
Это просто предыдущая картинка, показанная с использованием другой
палитры. |
 |
| Origin: Е. Федер "Фракталы", пер. с англ. - М: Мир, 1991,
стр 42-43. |
Картинка для этого фрактального кластера получена следующим образом.
Фиксируется окружность большого радиуса, и в ее центре помещается одна
частица - зародыш. На окружности случайным образом выбирается точка, в нее
помещается новая частица, и она начинает двигаться по направлению к
предыдущей активной частице. Соприкасаясь с кластером, частица
прилипает к нему, после чего из новой наугад выбранной точки на окружности
начинает двигаться следующая частица. |
 |
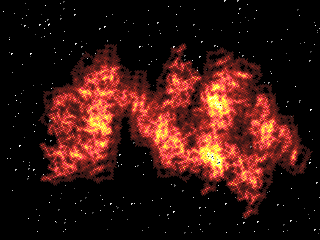
Похоже на голубую пену, не правда ли? Делается эта картинка очень
просто. На экран помещается 300 точек разной яркости, после чего они
одновременно начинают расти: вокруг каждой из точек пририсовываются
окружности всё увеличивающегося радиуса и уменьшающейся яркости. Точка
перестает расти, когда яркость внешней окружности уменьшается до нуля.
Если оказывается, что пиксел должен быть закрашен одновременно разными
цветами, выбирается цвет с большей яркостью. Вот и всё!
|

 |
Знаете ли вы, что такое последовательность Морса? Сейчас
объясню. Пишем цифру 0. Потом приписываем в конец написанной
последовательности уже написанные к этому моменту цифры, но вместо каждой
цифры 0 пишем цифру 1 и наоборот. Эту процедуру повторяем до
бесконечности. Полученная последовательность цифр
0110100110010110... и называется
последовательностью Морса. Кстати, ее можно получить и другим способом.
Пишем цифру 0. Потом в написанном числе каждую цифру 0 заменяем на 01, а
каждую цифру 1 на 10. Эту процедуру повторяем до
бесконечности.
Картинки же получены с помощью последовательности Морса
следующим образом. Последовательность Морса разбиваем на группы по три
цифры: 011 010 011 001 011 0... Может получиться 6 комбинаций (все, кроме
000 и 111). Отметим, что комбинации появляются с различной частотой.
Каждой из комбинаций сопоставляется поворот на угол, кратный
45o. Так, например, нижняя картинка получается, если выбрать
такие значения (+1 означает поворот на 45o против часовой
стрелки, и т.д.)

| 001 |
010 |
011 |
100 |
101 |
110 |
| +1 |
+1 |
+3 |
+3 |
-2 |
+1 | | Вот алгоритм
получения картинки. На экран ставим точку, и выбираем направление равным
0o (вправо). Берём очередную тройку цифр из последовательности Морса;
направление изменяем на соответствующий угол; перемещаемся от предыдущей точки
на расстояние одной точки в полученном направлении; ставим там точку. Повторяем
процедуру.
Таким образом, каждый раз новая точка является одной из восьми
точек, соседних с предыдущей точкой. Если оказывается, что точка уже отмечена,
её цвет увеличивается на 1. (А звёзды на нижней картинке - это просто
декоративный элемент).
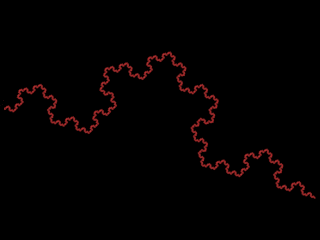 |
"Да
это же просто триадная кривая Кох," - скажете вы. Факт. Это действительно
триадная кривая Кох. Но зато получена она из последовательности Морса с
помощью алгоритма, описанного выше! Параметры для поворотов выбраны
следующими:

| 001 |
010 |
011 |
100 |
101 |
110 |
| -3 |
-3 |
+2 |
-3 |
+2 |
+2 | 
(Приведённая здесь
картинка в 2,5 раза меньше оригинала). Вот так вот! А я пока расскажу, что
такое кривая Кох. | Возьмём отрезок единичной длины и
разделим его на три равные части. На среднем отрезке как на основании построим
равносторонний треугольник, а основание выбросим. Получится ломаная, состоящая
из 4 отрезков. К каждому из полученных отрезков применим вышеописанную
процедуру. И т.д.

 |
| Ref: В мире науки, ©11, 1986, стр 92. |
Такого рода картинки получаются следующим образом. Начальные значения
x и y принимаются равными 0, ставится точка с координатами
.gif) , после
чего вычисляются новые значения координат по формуле: , после
чего вычисляются новые значения координат по формуле:
И т.д. Если точка, которую надо отметить, уже
отмечена, то ее цвет увеличивается на 1. В зависимости от разных значений
a, b, c получаются различные узоры.
|
|
|







.gif)
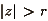 ). Здесь
). Здесь 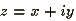 - комплексное
число, соответствующее точке
- комплексное
число, соответствующее точке .gif) . Множество
Жюлиа - это множество таких точек, что отображения вида
. Множество
Жюлиа - это множество таких точек, что отображения вида