Обзор алгоритмов сжатия без потерь

Арифметическое кодирование

Арифметическое кодирование является методом, позволяющим упаковывать символы входного алфавита без потерь при условии, что известно распределение частот этих символов. Арифметическое кодирование является оптимальным, достигая теоретической границы степени сжатия. Арифметическое кодирование – блочное и выходной код является уникальным для каждого из возможных входных сообщений; его нельзя разбить на коды отдельных символов, в отличие от кодов Хаффмана, которые являются неблочными, т.е. каждой букве входного алфавита ставится в соответствие определенный выходной код.

Текст, сжатый арифметическим кодером, рассматривается как некоторая двоичная дробь из интервала [0, 1). Результат сжатия можно представить как последовательность двоичных цифр из записи этой дроби. Каждый символ исходного текста представляется отрезком на числовой оси с длиной, равной вероятности его появления и началом, совпадающим с концом отрезка символа, предшествующего ему в алфавите. Сумма всех отрезков, очевидно должна равняться единице. Если рассматривать на каждом шаге текущий интервал как целое, то каждый вновь поступивший входной символ “вырезает” из него подинтервал пропорционально своей длине и положению.

Построение интервала для сообщения "АБВГ...":

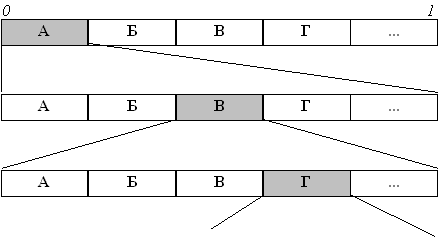
Поясним работу метода на примере:

Пусть алфавит состоит из двух символов: “a” и “b” с вероятностями соответственно 3/4 и 1/4.

Рассмотрим (открытый справа) интервал [0, 1). Разобьем его на части, длина которых пропорциональна вероятностям символов. В нашем случае это [0, 3/4) и [3/4, 1). Суть алгоритма в следующем: каждому слову во входном алфавите соответствует некоторый подинтервал из [0, 1). Пустому слову соответствует весь интервал [0, 1). После получения каждого очередного символа арифметический кодер уменьшает интервал, выбирая ту его часть, которая соответствует вновь поступившему символу. Кодом сообщения является интервал, выделенный после обработки всех его символов, точнее, число минимальной длины, входящее в этот интервал. Длина полученного интервала пропорциональна вероятности появления кодируемого текста.

Выполним алгоритм для цепочки “aaba”:

На первом шаге мы берем первые 3/4 интервала, соответствующие символу "а", затем оставляем от него еще только 3/4. После третьего шага от предыдущего интервала останется его правая четверть в соответствии с положением и вероятностью символа "b". И, наконец, на четвертом шаге мы оставляем лишь первые 3/4 от результата. Это и есть интервал, которому принадлежит исходное сообщение.

В качестве кода можно взять любое число из диапазона, полученного на шаге 4. Возникает вопрос: "А где же здесь сжатие? Исходный текст можно было закодировать четырьмя битами, а мы получили восьмибитный интервал". Дело в том, что в качестве кода мы можем выбрать, например, самый короткий код из интервала, равный 0.1 и получить четырехкратное сокращение объема текста. Для сравнения, код Хаффмана не смог бы сжать подобное сообщение, однако, на практике выигрыш обычно невелик и предпочтение отдается более простому и быстрому алгоритму из предыдущего раздела.

Арифметический декодер работает синхронно с кодером: начав с интервала [0, 1), он последовательно определяет символы входной цепочки. В частности, в нашем случае он вначале разделит (пропорционально частотам символов) интервал [0, 1) на [0, 0.11) и [0.11, 1). Поскольку число 0.1 (переданный кодером код цепочки "aaba") находится в первом из них, можно получить первый символ: "a". Затем делим первый подинтервал [0, 0.11) на [0, 0.1001) и [0.1001, 0.1100) (пропорционально частотам символов). Опять выбираем первый, так как 0 < 0.1 < 0.1001. Продолжая этот процесс, мы однозначно декодируем все четыре символа.

При рассмотрении этого метода возникают две проблемы: во-первых, необходима вещественная арифметика, вообще говоря, неограниченной точности, и во-вторых, результат кодирования становится известен лишь при окончании входного потока. Дальнейшие исследования, однако, показали, что можно практически без потерь обойтись целочисленной арифметикой небольшой точности (16-32 разряда), а также добиться инкрементальной работы алгоритма: цифры кода могут выдаваться последовательно по мере чтения входного потока.

Подобно алгоритму Хаффмана, арифметический кодер также является двухпроходным и требует передачи вместе с закодированным текстом еще и таблицы частот символов. Вообще, эти алгоритмы очень похожи и могут легко взаимозаменяться. Следовательно, существует адаптивный алгоритм арифметического кодирования со всеми вытекающими достоинствами и недостатками. Его основное отличие от статического в том, что новые интервалы вероятности перерассчитываются после получения каждого следующего символа из входного потока.