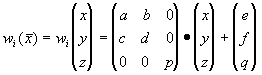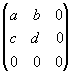Обзор алгоритмов сжатия с потерями

Фрактальный алгоритм

История фрактального сжатия

Рождение фрактальной геометрии обычно связывают с выходом в 1977 году книги Б. Мандельброта "Фрактальная геометрия природы". Одна из основных идей книги заключалась в том, что средствами традиционной геометрии (то есть используя линии и поверхности), чрезвычайно сложно представить природные объекты. Фрактальная геометрия задает их очень просто.

В 1981 году Джон Хатчинсон опубликовал статью "Фракталы и самоподобие", в которой была представлена теория построения фракталов с помощью системы итерируемых функций (IFS, Iterated Function System). Четыре года спустя появилась статья Майкла Барнсли и Стефана Демко, в которой приводилась уже достаточно стройная теория IFS. В 1987 году Барнсли основал Iterated Systems, компанию, основной деятельностью которой является создание новых алгоритмов и ПО с использованием фракталов. Всего через год, в 1988 году, он выпустил фундаментальный труд "Фракталы повсюду". Помимо описания IFS, в ней был получен результат, известный сейчас как Collage Theorem, который лежит в основе математического обоснования идеи фрактальной компрессии.

Если построение изображений с помощью фрактальной математики можно назвать прямой задачей, то построение по изображению IFS – это обратная задача. Довольно долго она считалась неразрешимой, однако Барнсли, используя Collage Theorem, построил соответствующий алгоритм. (В 1990 и 1991 годах эта идея была защищена патентами.) Если коэффициенты занимают меньше места, чем исходное изображение, то алгоритм является алгоритмом архивации.

Первая статья об успехах Барнсли в области компрессии появилась в журнале BYTE в январе 1988 года. В ней не описывалось решение обратной задачи, но приводилось несколько изображений, сжатых с коэффициентом 1:10000, что было совершенно ошеломительно. Но практически сразу было отмечено, что несмотря на броские названия ("Темный лес", "Побережье Монтере", "Поле подсолнухов") изображения в действительности имели искусственную природу. Это, вызвало массу скептических замечаний, подогреваемых еще и заявлением Барнсли о том, что "среднее изображение требует для сжатия порядка 100 часов работы на мощной двухпроцессорной рабочей станции, причем с участием человека".

Отношение к новому методу изменилось в 1992 году, когда Арнауд Джеквин, один из сотрудников Барнсли, при защите диссертации описал практический алгоритм и опубликовал его. Этот алгоритм был крайне медленным и не претендовал на компрессию в 10000 раз (полноцветное 24-разрядное изображение с его помощью могло быть сжато без существенных потерь с коэффициентом 1:8 - 1:50); но его несомненным достоинством было то, что вмешательство человека удалось полностью исключить. Сегодня все известные программы фрактальной компрессии базируются на алгоритме Джеквина. В 1993 году вышел первый коммерческий продукт компании Iterated Systems. Ему было посвящено достаточно много публикаций, но о коммерческом успехе речь не шла, продукт был достаточно "сырой", компания не предпринимала никаких рекламных шагов, и приобрести программу было тяжело.

В 1994 году Ювал Фишер были предоставил во всеобщее пользование исходные тексты исследовательской программы, в которой использовалось разложение изображения в квадродерево и были реализованы алгоритмы оптимизации поиска. Позднее появилось еще несколько исследовательских проектов, которые в качестве начального варианта программы использовали программу Фишера. В июле 1995 года в Тронхейме (Швеция) состоялась первая школа-конференция, посвященная фрактальной компрессии.

Идея метода

Фрактальная архивация основана на том, что мы представляем изображение в более компактной форме – с помощью коэффициентов системы итерируемых функций (Iterated Function System – далее по тексту как IFS). Строго говоря, IFS представляет собой набор трехмерных аффинных преобразований, в нашем случае переводящих одно изображение в другое. Преобразованию подвергаются точки в трехмерном пространстве (х_координата, у_координата, яркость).

Наиболее наглядно этот процесс продемонстрировал Барнсли в своей книге "Fractal Image Compression". Там введено понятие Фотокопировальной Машины, состоящей из экрана, на котором изображена исходная картинка, и системы линз, проецирующих изображение на другой экран:

• Линзы могут проецировать часть изображения произвольной формы в любое другое место нового изображения.
• Области, в которые проецируются изображения, не пересекаются.
• Линза может менять яркость и уменьшать контрастность.
• Линза может зеркально отражать и поворачивать свой фрагмент изображения.
• Линза должна масштабировать (уменьшать) свой фрагмент изображения.

Расставляя линзы и меняя их характеристики, мы можем управлять получаемым изображением. Одна итерация работы машины заключается в том, что по исходному изображению с помощью проектирования строится новое, после чего новое берется в качестве исходного. Утверждается, что в процессе итераций мы получим изображение, которое перестанет изменяться. Оно будет зависеть только от расположения и характеристик линз, и не будет зависеть от исходной картинки. Это изображение называется "неподвижной точкой" или аттрактором данной IFS. Соответствующая теория гарантирует наличие ровно одной неподвижной точки для каждой IFS.

Поскольку отображение линз является сжимающим, каждая линза в явном виде задает самоподобные области в нашем изображении. Благодаря самоподобию мы получаем сложную структуру изображения при любом увеличении. Таким образом, интуитивно понятно, что система итерируемых функций задает фрактал (нестрого – самоподобный математический объект).

Наиболее известны два изображения, полученных с помощью IFS: "треугольник Серпинского" и "папоротник Барнсли".

Папоротник Барнсли. Задается 4 преобразованиями.

Треугольник Серпинского. Задается 3 преобразованиями.

"Треугольник Серпинского" задается тремя, а "папоротник Барнсли" четырьмя аффинными преобразованиями (или, в нашей терминологии, "линзами"). Каждое преобразование кодируется считанными байтами, в то время как изображение, построенное с их помощью, может занимать и несколько мегабайт.

Из вышесказанного становится понятно, как работает архиватор, и почему ему требуется так много времени. Фактически, фрактальная компрессия – это поиск самоподобных областей в изображении и определение для них параметров аффинных преобразований.

В худшем случае, если не будет применяться оптимизирующий алгоритм, потребуется перебор и сравнение всех возможных фрагментов изображения разного размера. Даже для небольших изображений при учете дискретности мы получим астрономическое число перебираемых вариантов. Причем, даже резкое сужение классов преобразований, например, за счет масштабирования только в определенное количество раз, не дает заметного выигрыша во времени. Кроме того, при этом теряется качество изображения. Подавляющее большинство исследований в области фрактальной компрессии сейчас направлены на уменьшение времени архивации, необходимого для получения качественного изображения.

Математические основы фрактального сжатия

Далее приводятся основные определения и теоремы, на которых базируется фрактальная компрессия.

Определение. Преобразование w:R² –> R², представимое в виде

где a, b, c, d, e, f действительные числа и (x y) принадлежит R² называется двумерным аффинным преобразованием.

Определение. Преобразование w:R³ –> R³, представимое в виде

где a, b, c, d, e, f, p, q, r, s, t, u действительные числа и (x y z) принадлежит R³ называется трехмерным аффинным преобразованием.

Определение. Пусть f:X –> X – преобразование в пространстве Х. Точка x_f принадлежащая X такая, что f(x_f)=x_f называется неподвижной точкой (аттрактором) преобразования.

Определение. Пусть f:X–>X в метрическом пространстве (Х, d) называется сжимающим, если существует число s: 0 <= s < 1, такое, что d(f(x),f(y)) <= s * d(x,y) длялюбых x,y принадлежащих X.

Замечание: формально можно использовать любое сжимающее отображение при фрактальной компрессии, но реально используются лишь трехмерные аффинные преобразования с достаточно сильными ограничениями на коэффициенты.

Теорема (О сжимающем преобразовании). Пусть f:X –> X в полном метрическом пространстве (Х, d). Тогда существует в точности одна неподвижная точка x_f принадлежащая X этого преобразования, и для любой точки x принадлежащей X последовательность {fⁿ(x): n=0,1,2…} сходится к x_f.

Более общая формулировка этой теоремы гарантирует нам сходимость.

Определение. Изображением называется функция S, определенная на единичном квадрате и принимающая значения от 0 до 1 или S(x,y) принадлежит [0...1] для любых x,y принадлежащих [0...1].

Пусть трехмерное аффинное преобразование w_f:R³ –> R³, записано в виде

и определено на компактном подмножестве D_i декартова квадрата [0..1]x[0..1]. Тогда оно переведет часть поверхности S в область R_i, расположенную со сдвигом (e,f) и поворотом, заданным матрицей

При этом, если интерпретировать значение S как яркость соответствующих точек, она уменьшится в p раз (преобразование обязано быть сжимающим) и изменится на сдвиг q.

Определение. Конечная совокупность W сжимающих трехмерных аффинных преобразований w_i, определенных на областях D_i, таких, что w_i(D_i) = R_i и пересечение R_i с R_j является пустым множеством, называется системой итерируемых функций (IFS).

Системе итерируемых функций однозначно сопоставляется неподвижная точка – изображение. Таким образом, процесс компрессии заключается в поиске коэффициентов системы, а процесс декомпрессии – в проведении итераций системы до стабилизации полученного изображения (неподвижной точки IFS). На практике бывает достаточно 7-16 итераций. Области R_i в именуются ранговыми, а области D_i – доменными.

Типовая схема фрактального сжатия

С учётом вышесказанного, схема компрессии выглядит так: изображение R разбивают на ранговые области R_i. Далее для каждой области R_i находят область D_i и преобразование w_i такие, что выполняются следующие условия:

1. D_i по размерам больше R_i.
2. w_i(R_i) имеет ту же форму, размеры и положение, что и R_i.
3. Коэффициент преобразования должен быть меньше единицы.
4. Значение должно быть как можно меньше.

Первые три условия означают, что отображение w_i будет сжимающим. А в силу четвёртого условия кодируемое изображение R и его образ W(R) будут похожи друг на друга. В идеале R = W(R). А это означает, что изображение R и будет являться неподвижной точкой W. Именно здесь используется подобие различных частей изображения. Как оказалось, практически все реальные изображения содержат такие похожие друг на друга, с точностью до аффинного преобразования, части.

Таким образом, для компрессии изображения W нужно:

1. Разбить изображение на ранговые области R_i (непересекающиеся области, покрывающие все изображение).
2. Для каждой ранговой области R_i найти область D_i, и отображение w_i, с указанными выше свойствами.
3. Запомнить коэффициенты аффинных преобразований W, положения доменных областей D_i, а также разбиение изображения на домены.

Соответственно, для декомпрессии изображения нужно будет:

1. Создать начальное изображение R₀.
2. Многократно применить к нему отображение W (объединение w_i).
3. Так как отображение W сжимающее, то в результате, после достаточного количества итераций, изображение придет к аттрактору и перестанет меняться. Аттрактор и является нашим исходным изображением. Декомпрессия завершена.

Сравнение с JPEG

Сегодня наиболее распространенным алгоритмом архивации графики является JPEG. Сравним его с фрактальной компрессией.

Во-первых, заметим, что и тот, и другой алгоритм оперируют 8-битными (в градациях серого) и 24-битными полноцветными изображениями. Оба являются алгоритмами сжатия с потерями и обеспечивают близкие коэффициенты архивации. И у фрактального алгоритма, и у JPEG существует возможность увеличить степень сжатия за счет увеличения потерь. Кроме того, оба алгоритма очень хорошо распараллеливаются.

Различия начинаются, если мы рассмотрим время, необходимое алгоритмам для архивации/разархивации. Так, фрактальный алгоритм сжимает в сотни и даже в тысячи раз дольше, чем JPEG. Распаковка изображения, наоборот, произойдет в 5-10 раз быстрее. Поэтому, если изображение будет сжато только один раз, а передано по сети и распаковано множество раз, то выгодней использовать фрактальный алгоритм.

JPEG использует разложение изображения по косинусоидальным функциям, поэтому потери в нем (даже при заданных минимальных потерях) проявляются в волнах и ореолах на границе резких переходов цветов. Именно за этот эффект его не любят использовать при сжатии изображений, которые готовят для качественной печати: там этот эффект может стать очень заметен. Фрактальный алгоритм избавлен от этого недостатка. Более того, при печати изображения каждый раз приходится выполнять операцию масштабирования, поскольку растр печатающего устройства не совпадает с растром изображения. При преобразовании также может возникнуть несколько неприятных эффектов, с которыми можно бороться либо масштабируя изображение программно, либо снабжая устройство печати своим процессором, винчестером и набором программ обработки изображений. Как можно догадаться, при использовании фрактального алгоритма таких проблем практически не возникает.

Вытеснение JPEG фрактальным алгоритмом в повсеместном использовании произойдет еще не скоро (хотя бы в силу низкой скорости архивации последнего), однако в области приложений мультимедиа, в компьютерных играх его использование вполне оправдано.

Характеристики фрактального алгоритма

Коэффициенты компрессии: 2-2000 (Задается пользователем).

Класс изображений: Полноцветные 24 битные изображения или изображения в градациях серого без резких переходов цветов (фотографии). Желательно, чтобы области большей значимости (для восприятия) были более контрастными и резкими, а области меньшей значимости — неконтрастными и размытыми.

Симметричность: 100-100000.

Характерные особенности: Может свободно масштабировать изображение при разархивации, увеличивая его в 2-4 раза без появления "лестничного эффекта". При увеличении степени компрессии появляется "блочный" эффект на границах блоков в изображении.