Обзор алгоритмов сжатия без потерь

Метод Хаффмана

Адаптивное сжатие Хаффмана

Следующим шагом в развитии алгоритма Хаффмана стала его адаптивная версия. Адаптивное сжатие Хаффмана позволяет не передавать модель сообщения вместе с ним самим и ограничиться одним проходом по сообщению как при кодировании, так и при декодировании. Практически любая форма кодирования может быть конвертирована в адаптивную. В общем случае программа, реализующая адаптивное сжатие, может быть выражена в следующей форме:

ИнициализироватьМодель();
Пока не конец сообщения
  Символ = ВзятьСледующийСимвол();
  Закодировать(Символ);
  ОбновитьМодельСимволом(Символ);
Конец пока;

Декодер в адаптивной схеме работает аналогичным образом:

ИнициализироватьМодель();
Пока не конец сжатой информации
  Символ = РаскодироватьСледующий();
  ВыдатьСимвол(Символ);
  ОбновитьМодельСимволом(Символ);
Конец пока;

Схема адаптивного кодирования/декодирования работает благодаря тому, что при кодировании, и при декодировании используются одни и те же процедуры "ИнициализироватьМодель" и "ОбновитьМодельСимволом" И компрессор, и декомпрессор начинают с "пустой" модели (не содержащей информации о сообщении) и с каждым просмотренным символом обновляют ее одинаковым образом.

Адаптивное кодирование Хаффмана

В создании алгоритма адаптивного кодирования Хаффмана наибольшие сложности возникают при разработке процедуры ОбновитьМодельСимволом(); можно было бы просто вставить внутрь этой процедуры полное построение дерева Хаффмана. В результате мы получили бы очень медленный алгоритм сжатия, так как построение дерева – это слишком большая работа и производить ее при обработке каждого символа неразумно. К счастью, существует способ модифицировать уже существующее дерево так, чтобы отобразить обработку нового символа.

Упорядоченное Дерево
Будем говорить, что дерево обладает свойством упорядоченности, если его узлы могут быть перечислены в порядке возрастания веса и в этом перечислении каждый узел находится рядом со своим братом. Пример упорядоченного дерева приведен на рисунке:

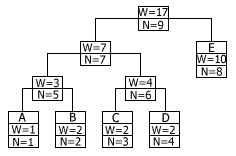
Здесь W – вес узла, N – порядковый номер в списке узлов.

Примем без доказательства утверждение о том, что двоичное дерево является деревом кодирования Хаффмана тогда и только тогда, когда оно удовлетворяет свойству упорядоченности. Сохранение свойства упорядоченности в процессе обновления дерева позволяет нам быть уверенным в том, что двоичное дерево, с которым мы работаем, – это дерево кодирования Хаффмана и до, и после обновления веса у листьев дерева. Обновление дерева при считывании очередного символа сообщения состоит из двух операций. Первая - увеличение веса узлов дерева – представлена на следующем рисунке.

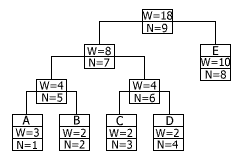
Вначале увеличиваем вес листа, соответствующего считанному символу, на единицу. Затем увеличиваем вес родителя, чтобы привести его в соответствие с новыми значениями веса у потомков. Этот процесс продолжается до тех пор, пока мы не доберемся до корня дерева. Среднее число операций увеличения веса равно среднему количеству битов, необходимых для того, чтобы закодировать символ.

Вторая операция – перестановка узлов дерева – требуется тогда, когда увеличение веса узла приводит к нарушению свойства упорядоченности, то есть тогда, когда увеличенный вес узла стал больше, чем вес следующего по порядку узла.

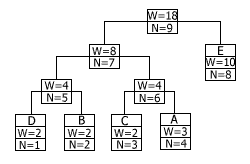
Если и дальше продолжать обрабатывать увеличение веса, двигаясь к корню дерева, то наше дерево перестанет быть деревом Хаффмана. Чтобы сохранить упорядоченность дерева кодирования, алгоритм работает следующим образом. Пусть новый увеличенный вес узла равен W+1. Тогда начинаем двигаться по списку в сторону увеличения веса, пока не найдем последний узел с весом W. Переставим текущий и найденный узлы между собой в списке, восстанавливая таким образом порядок в дереве.

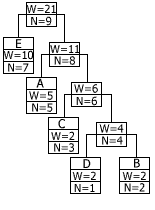
При этом родители каждого из узлов тоже изменяются. На этом операция перестановки заканчивается. После перестановки операция увеличения веса узлов продолжается дальше.

Следующий узел, вес которого будет увеличен алгоритмом, – это новый родитель узла, увеличение веса которого вызвало перестановку. Предположим, что символ A встретился в сообщении еще два раза подряд. Дерево кодирования после двукратного вызова процедуры обновления показано на рисунке:

Обратите внимание, как обновление дерева кодирования отражается на длине кодов Хаффмана для входящих в данное сообщение символов. В целом алгоритм обновления дерева может быть записан следующим образом:

Алгоритм обновления дерева

ОбновитьМодельСимволом(Символ)
{
  ТекущийУзел = ЛистСоответствующий(Символ);
  Всегда
  УвеличитьВес(ТекущийУзел);
  Если ТекущийУзел = КореньДерева
    Выход;
  Если Вес(ТекущийУзел) > Вес(СледующийЗа(ТекущийУзел))
    Перестановка();
  ТекущийУзел = Родитель(ТекущийУзел);
  Конец Всегда;
}

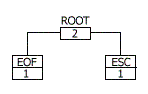
Проблемы адаптивного кодирования

Хорошо было бы, чтобы кодер не тратил зря кодовое пространство на символы, которые не встречаются в сообщении. Если речь идет о классическом алгоритме Хаффмана, то те символы, которые не встречаются в сообщении, уже известны до начала кодирования, так как известна таблица частот и символы, у которых частота встречаемости равна 0. В адаптивной версии алгоритма мы не можем знать заранее, какие символы появятся в сообщении. Можно проинициализировать дерево Хаффмана так, чтобы оно имело все 256 символов алфавита (для 8-и битовых кодов) с частотой, равной 1. В начале кодирования каждый код будет иметь длину 8 битов. По мере адаптации модели наиболее часто встречающиеся символы будут кодироваться все меньшим и меньшим количеством битов. Такой подход работоспособен, но он значительно снижает степень сжатия, особенно на коротких сообщениях.

Лучше начинать моделирование с пустого дерева и добавлять в него символы только по мере их появления в сжимаемом сообщении. Но это приводит к очевидному противоречию: когда символ появляется в сообщении первый раз, он не может быть закодирован, так как его еще нет в дереве кодирования.

Чтобы разрешить это противоречие, введем специальный ESCAPE код, который будет означать, что следующий символ закодирован вне контекста модели сообщения. Например, его можно передать в поток сжатой информации как есть, не кодируя вообще. Метод "ЗакодироватьСимвол" в алгоритме адаптивного кодирования Хаффмана можно записать следующим образом:

ЗакодироватьСимвол(Символ)
{
  Если СимволУжеЕстьВТаблице(Символ)
  ВыдатьКодХаффманаДля(Символ);
  Иначе
  {
    ВыдатьКодХаффманаДля(ESC);
    ВыдатьСимвол(Символ);
  }
}

Использование специального символа ESC подразумевает определенную инициализацию дерева до начала кодирования и декодирования: в него помещаются 2 специальных символа: ESC и EOF (конец файла), с весом, равным 1.

Поскольку процесс обновления не коснется их веса, то по ходу кодирования они будут перемещаться на самые удаленные ветви дерева и иметь самые длинные коды.